Quasicrystals: Symmetry and Characteristics and Their Application as an Art Form
Part of artist M.C. Escher’s work focused on tessellations in the second dimension, many of which would periodically tile the plane. However, tilings can also be aperiodic, not having a set repeating pattern. Roger Penrose and his Penrose tilings are examples of these types of tiles. Penrose tilings have another characteristic about them as well: they are also quasicrystals. A quasicrystal is an ordered, non-periodic structure, which differs crystals that do have periodic structure. These quasicrystals also exist in the third dimension, and there is “an infinite set of 2D and 3D lattices that exhibit self-similarity properties of a crystal, but have quasiperiodic, rather than periodic, translational order” [1].
As with two dimensional tessellations, groups and the symmetries they are characterized by play an important role. For crystals, rotational symmetry must be of a fold number k, where k ∈ {1,2,3,4,6} in the second and third dimensions. This is known as the crystallographic restriction [2]. However, a specific crystal produced by Peter Kramer in 1984 icosahedral symmetry, which is not allowed under this crystallographic restriction [3]. This crystal became known as the quasicrystal, or quasiperiodic crystal, due to its quasiperiodic nature resulting from the symmetry group it is in. Quasicrystals are able to fill space, as they can be tessellations. Yet, they do not have translational symmetry, like Penrose tilings.
Quasicrystals also exhibit some other interesting properties. Second and third dimensional quasicrystals are shown to be projections from higher dimensional structures. One example of this is of De Brujin proving Penrose tilings to be planar projections of hypercubic tessellations, namely that of 5 space [3]. Electron diffraction patterns for icosahedral quasicrystals show 10-fold diffraction patterns, in which inflation symmetry can be seen [1].
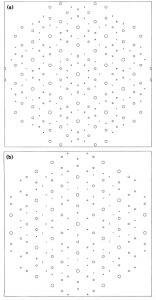
Figure 1. Diffraction patterns of various quasicrystals. The top icosahedral quasicrystal contains pentagonal shapes, which inflate out from the center [1]
These quasicrystal shapes have inspired the mathematician Tony Robbin to create art with these shapes, namely that of sculptures [4]. These sculptures would need to exist within space, however, so their rigidity needed to be taken into account. In order to create the quasicrystals with enough support, computer programs were used to identify the hidden makeup behind the “seemingly random patterns.” One such sub structure was that of parallel ribbons that adjacent cells have with one another, which are called multigrids, and are residues of the higher dimensional shapes that produce quasicrystals. The multigrids can then be used to identify where to place braces in the structure to give it support. Along with other characteristics of the quasicrystals, Robbin was able to produce large scale version in space. In this way, the mathematical analysis of the structures is used to inform the art and its creation.
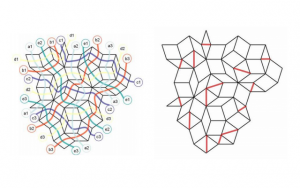
Figure 2. The ribbon multigrids of a quasicrystal, as well as sites for braces in a three dimensional model [4].
References:
[1] Levine, Dov, and Paul Joseph Steinhardt. “Quasicrystals: a new class of ordered structures.” Physical review letters 53.26 (1984): 2477.
[2] Baake, Michael. “A guide to mathematical quasicrystals.” Quasicrystals. Springer Berlin Heidelberg, 2002. 17-48.
[3] Senechal, Marjorie. “Coxetering Crystals.” Renaissance Banff: Mathematics, Music, Art, Culture. Bridges Conference, 2005.
[4] Robbin, Tony. “The Visual and Structural Porperties of Quasicrystals.” Proceedings of the International Conference Transformables. 2013.
[5] Kramer, Peter, and Roberto Neri. “On periodic and non-periodic space fillings of Em obtained by projection.” Acta Crystallographica Section A: Foundations of Crystallography 40.5 (1984): 580-587.


